Hello!

I am a PhD candidate in the University of Michigan’s Industrial and Operations Engineering department. My research centers discrete optimization and approximation algorithms. I started my work in Michigan with developing exact algorithms for the Maximum-Entropy Sampling Problem (MESP), an NP-Hard problem. Motivated by an environmental design problem, the MESP seeks to find the most informative subset of sensors in a sensor network. I have worked on compiling data that we can use as input to test the lower and upper bounds of the model. My current work focused on stochastic variants of combinatorial optimization problems like the set cover problem and the minimum element problem. My goal is to improve current theoretical guarantees for this combinatorial optimization problem. My dissertation work covers:

I will be graduating in December and hope to be joining an institute with a thriving research environment.

When I'm not doing research, I like to be outdoors hiking, climbing or whatever the local environment has to offer.

Featured Publications

Minimum cost adaptive submoduler cover

H Al-Thani, Y Cui, V Nagarajan

Submitted 2024, Mathematics of Operations Research

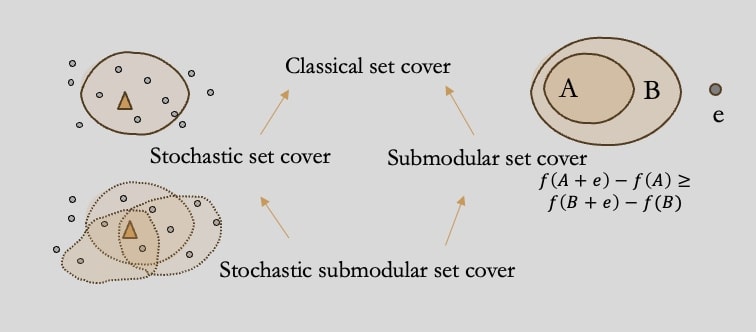
We address the minimum cost cover problem of adaptive-submodular functions and introduce a 4(1+lnQ)-approximation algorithm, where Q represents the target value. Additionally, we tackle a more comprehensive objective: minimizing the p-th moment of the coverage cost. Our results demonstrate that our algorithm provides a (p+1)^{p+1}(lnQ +1)^p) approximation guarantee for all p ≥ 1. Adaptive submodularity is a crucial concept in stochastic optimization, relevant to various fields including sensor placement, hypothesis identification, and viral marketing.

Tridiagonal maximum-entropy sampling and tridiagonal masks

H Al-Thani, J Lee

Published 2023, Discrete Applied Mathematics

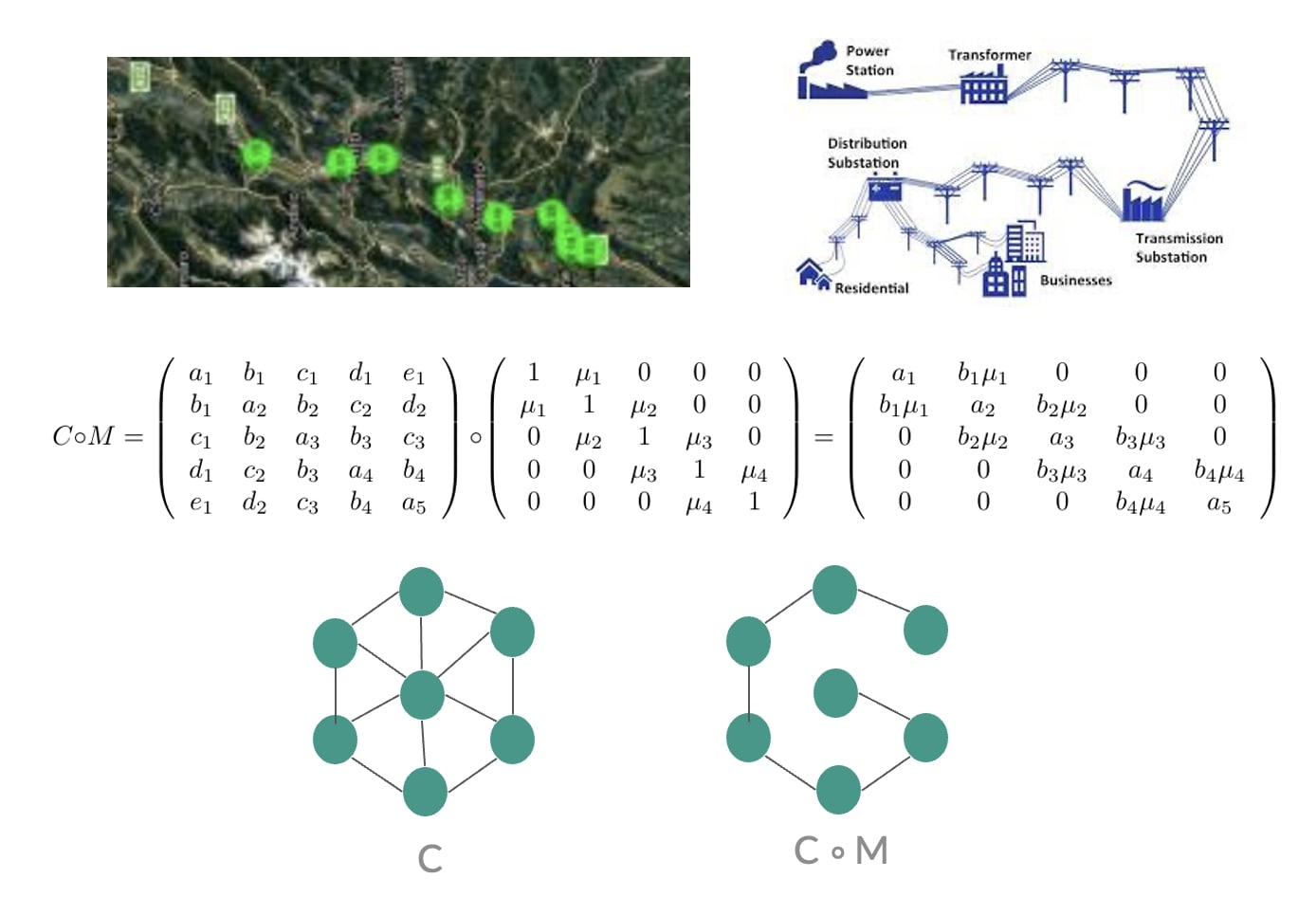
We present exact solutions to specific cases of the maximum-entropy sampling problem where the covariance matrix is tridiagonal or has a structure induced by a spider graph. We also present a condition where the MESP can be solved exactly for arrowhead matricies, that are generally know to be NP-hard.

Full List of Publications

Featured GitHub Projects

OpenStreetMap ShinyApp for manufactured housing communities in Michigan

H Al-Thani, N Shi, B Xiang

Online 2024

Manufactured housing communities occupy an important and unique space in the US housing market. They are known to be the cheapest strata of housing available for low-income families and vulnerable groups such as veterans and seniors with a fixed income. Manufactured Hosuing Action is an organized movement of manufactured home (MH) residents that advocate for policy changes that protect MH residents and the vulnerable groups among them. They asked our team to collect and display data in a way that can communicate to policy makers the number of people in their district affected by predatory real-estate practices.

R Package for matrix generation for the maximum-entropy sampling problem

H Al-Thani, J Lee

Online 2021

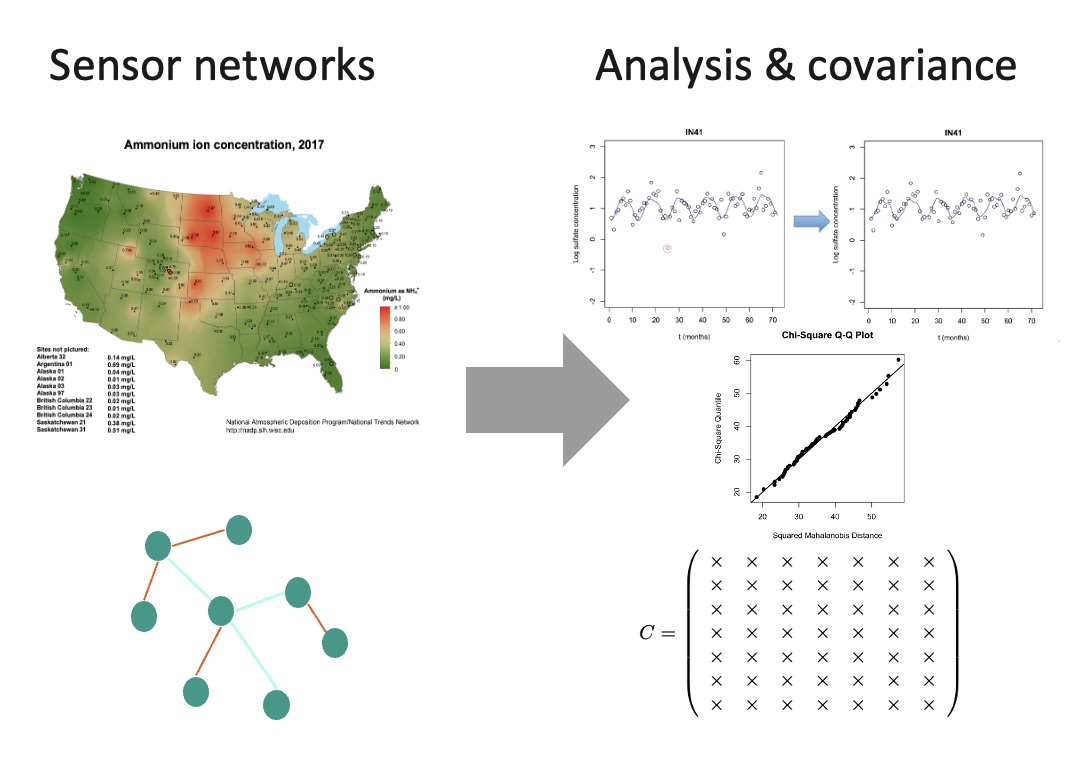
We present an R package that generates covariance matrices to be used as input for the maximum-entropy sampling problem (MESP). The MESP models the situation where there is some set of observable streams of information but only k < n can be observed, the goal is to find the k most informative subset using the covariance matrix generated from the data. The covariance matrix is required to be drawn from a Gaussian distribution, the R package is equipped with analytics that analyse the distribution of a chemistry dataset and applies a generalized model based on prior work to deseaonsalize and detrend the dataset.